History

Newton, in the Principia, hinted at angular momentum in his examples of the First Law of Motion,

A top, whose parts by their cohesion are perpetually drawn aside from rectilinear motions, does not cease its rotation, otherwise than as it is retarded by the air. The greater bodies of the planets and comets, meeting with less resistance in more free spaces, preserve their motions both progressive and circular for a much longer time.

He did not further investigate angular momentum directly in the Principia,

From such kind of reflexions also sometimes arise the circular motions of bodies about their own centres. But these are cases which I do not consider in what follows; and it would be too tedious to demonstrate every particular that relates to this subject.

However, his geometric proof of the law of areas is an outstanding example of Newton's genius, and indirectly proves angular momentum conservation in the case of a central force.

The Law of Areasedit

Newton's derivationedit

As a planet orbits the Sun, the line between the Sun and the planet sweeps out equal areas in equal intervals of time. This had been known since Kepler expounded his second law of planetary motion. Newton derived a unique geometric proof, and went on to show that the attractive force of the Sun's gravity was the cause of all of Kepler's laws.

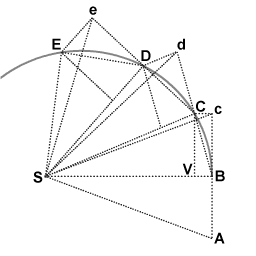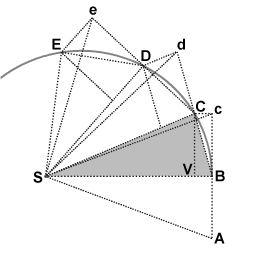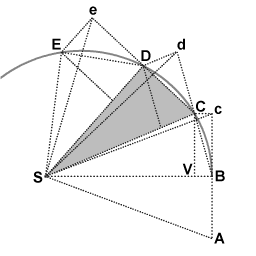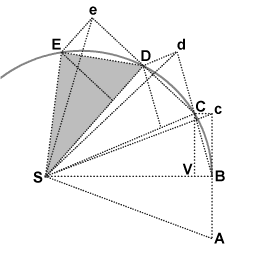
During the first interval of time, an object is in motion from point A to point B. Undisturbed, it would continue to point c during the second interval. When the object arrives at B, it receives an impulse directed toward point S. The impulse gives it a small added velocity toward S, such that if this were its only velocity, it would move from B to V during the second interval. By the rules of velocity composition, these two velocities add, and point C is found by construction of parallelogram BcCV. Thus the object's path is deflected by the impulse so that it arrives at point C at the end of the second interval. Because the triangles SBc and SBC have the same base SB and the same height Bc or VC, they have the same area. By symmetry, triangle SBc also has the same area as triangle SAB, therefore the object has swept out equal areas SAB and SBC in equal times.

At point C, the object receives another impulse toward S, again deflecting its path during the third interval from d to D. Thus it continues to E and beyond, the triangles SAB, SBc, SBC, SCd, SCD, SDe, SDE all having the same area. Allowing the time intervals to become ever smaller, the path ABCDE approaches indefinitely close to a continuous curve.

Note that because this derivation is geometric, and no specific force is applied, it proves a more general law than Kepler's second law of planetary motion. It shows that the Law of Areas applies to any central force, attractive or repulsive, continuous or non-continuous, or zero.

Conservation of angular momentum in the Law of Areasedit

The proportionality of angular momentum to the area swept out by a moving object can be understood by realizing that the bases of the triangles, that is, the lines from S to the object, are equivalent to the radius r, and that the heights of the triangles are proportional to the perpendicular component of velocity v_⊥. Hence, if the area swept per unit time is constant, then by the triangular area formula 1/2(base)(height), the product (base)(height) and therefore the product rv_⊥ are constant: if r and the base length are decreased, v_⊥ and height must increase proportionally. Mass is constant, therefore angular momentum rmv_⊥ is conserved by this exchange of distance and velocity.

In the case of triangle SBC, area is equal to 1/2(SB)(VC). Wherever C is eventually located due to the impulse applied at B, the product (SB)(VC), and therefore rmv_⊥ remain constant. Similarly so for each of the triangles.

After Newtonedit

Leonhard Euler, Daniel Bernoulli, and Patrick d'Arcy all understood angular momentum in terms of conservation of areal velocity, a result of their analysis of Kepler's second law of planetary motion. It is unlikely that they realized the implications for ordinary rotating matter.

In 1736 Euler, like Newton, touched on some of the equations of angular momentum in his Mechanica without further developing them.

Bernoulli wrote in a 1744 letter of a "moment of rotational motion", possibly the first conception of angular momentum as we now understand it.

In 1799, Pierre-Simon Laplace first realized that a fixed plane was associated with rotation—his invariable plane.

Louis Poinsot in 1803 began representing rotations as a line segment perpendicular to the rotation, and elaborated on the "conservation of moments".

In 1852 Léon Foucault used a gyroscope in an experiment to display the Earth's rotation.

William J. M. Rankine's 1858 Manual of Applied Mechanics defined angular momentum in the modern sense for the first time:

...a line whose length is proportional to the magnitude of the angular momentum, and whose direction is perpendicular to the plane of motion of the body and of the fixed point, and such, that when the motion of the body is viewed from the extremity of the line, the radius-vector of the body seems to have right-handed rotation.

In an 1872 edition of the same book, Rankine stated that "The term angular momentum was introduced by Mr. Hayward," probably referring to R.B. Hayward's article On a Direct Method of estimating Velocities, Accelerations, and all similar Quantities with respect to Axes moveable in any manner in Space with Applications, which was introduced in 1856, and published in 1864. Rankine was mistaken, as numerous publications feature the term starting in the late 18th to early 19th centuries. However, Hayward's article apparently was the first use of the term and the concept seen by much of the English-speaking world. Before this, angular momentum was typically referred to as "momentum of rotation" in English.